A Penny in Free Fall
A Research Study by Grant Macklem and Nathan Janos
1997
With the Experimental Aid of
Sam Barranco, Jeff Jagunich, Aditya Nagrath, and Alan Schmidt
INTRODUCTION
This research is a study of whether a penny would kill a person if it landed on them
after falling from the Empire State building (a height of 1,453 feet). For almost 6 years, proving the answer
to this question has been puzzling both my partner and I. After developing a stronger math and science
background in high school, we decided to tackle this problem. None of the formulae we had seen before was
relevant to the practical side of the problem. That is, they did not take into account the fact that a penny
will turn in the air and that the changing aerodynamics and surface area will affect its velocity. We finally
stumbled onto some formulas that were related to the hyperbolic trigonometric functions and the problem was
thought to be much easier. We also looked through several physics books for equations that involve drag. After
we found some, the same equations were found on the HP-48 series calculator.
Note that there are two different types of pennies in existence. Pennies made before
1982 are 95% copper and 5% zinc. After 1982, production of that penny stopped and a new penny was introduced.
This new penny is 97.5% zinc and 2.5% copper. It weighs only 2.500 grams compared to the old penny weighing
3.110 grams. The difference in mass is 0.61 grams. This is equivalent to 19.61% of the mass of the old penny
and 24.4% of the mass of the new penny. Thus, in order to assure accurate results, make sure to experiment
with pennies produced after 1983 and before 1981, but obviously not during the same trial. The treasury
department has removed the original web page providing numbers, but for the next closest document, see [1].
You and your partner will inevitably want to develop some sort of hand signals so that
you will be able to communicate with each other. For example, when over 50 feet separates you and your partner,
vocal communication is not very effective. If you are indoors and such a distance separates you, echoes become
a major problem. It is possible to use only hand signals for this experiment. One type could mean stop the
stopwatch while another means ready. However, if you have 2-way radios, your partner can relay the falling time
back to you, you can then both record the times, and compare any discrepancies later. Plus, you can relay
information about a perfect drop versus one that was obstructed or tell your partner about problems you had not
anticipated and consequently did not develop hand signals for.
The use of a high structure is necessary because it is fun to drop things from great
heights. Seriously, though, the height plays a significant role in the accuracy of the measurements. If the
distance is too short, the ground partner will have hardly noticed the stopwatch is running and will
immediately need to concentrate on stopping it. However, if you use too high of a structure, this can also
prove ineffective. The ground partner will become impatient and stop the stopwatch too early in anticipation
of the penny colliding with the earth. The structure you decide to use should be at least 40 in
height.
You should be cautious and aware of both horizontal and vertical wind drafts in the
area where you plan to drop the pennies. The reader may recall from classical (or Newtonian) physics that the
horizontal motion of a projectile does not affect the falling time. However, in the real world, there is air
resistance. As such, any deviation from a purely vertical fall will affect the falling time. If in doubt, refer
to Pythagoras who tells us that if the pennys trajectory has a horizontal component from the wind, it will have
to fall a greater distance through the air. Thus, there is more resistance in the fall. This resultant motion
determines the terminal velocity. If a strong horizontal wind exists, the penny will move too far to the side
and it will seem to fall rather slowly toward the earth. The vertical speed is also inevitably linked to the
relative speed of the penny with the air. Because this relative speed will always be the same, vertical
air drafts will change the speed relative to the stationary surroundings.
Be aware of the surroundings, also. Pennies do not fall straight down; they flutter
around in the air while they fall. This could potentially be dangerous for observers or objects the penny may
hit. Thus, make sure there is a wide enough area for the penny to fall. This way, the penny will reach the
ground without its speed or trajectory changed by any external factor.
It is important to use an accurate timing device, but too accurate will not be any
better. In other words, a second hand on a wristwatch will not be accurate enough but anything more accurate
than hundredths of a second will be too accurate. This is because the falling times of the penny will vary in
the hundredths range making more digits useless. The actual terminal velocity of the penny could also be
argued over. Since it changes minutely due to its own rotation, it will never achieve a single, terminal
speed. However, the speed, averaged over the rotations of the penny, will be close to the same number every
time.
PROBLEM: If a penny fell of the Empire State Building and hit a person in the skull, would it
kill them?
HYPOTHESIS: Depending on where the penny hits, the force of the penny will overcome the
protective skull and kill the person.
MATERIALS:
- Stopwatch With Start and Pause Buttons
- 50+ Measuring Tape
- Weight
- Solder
- Wire Strippers/Cutters
- 10+ Pre-1982 Pennies
- 10+ Post-1982 Pennies
- 10+ 3/8" Ball Bearings
- ¼" Drill Bit
- Thermometer
|
- 2 Separately Insulated 100+ Lengths of Wire
- 100 String
- Soldering Iron
- Large Spool or Dowel (2"+ diameter)
- Electrical Tape
- 2 Two-way Radios (optional)
- Momentary Push-button Switch (RS# 275-618A)
- Electric Hand-Held Drill
- 3/8" Drill Bit
- Small Pill Container or Experimenter Box
|

PROCEDURE:
- Take apart the stopwatch (a simple one with well-defined click buttons as shown is preferred). Be careful
not to lose any parts, as the watch will be reassembled later. Locate the area where the end of the start/stop
button is. You should find two metal plates that connect when the button is pressed. Carefully solder either
leads or the ends of the 100 lengths of wire to each metal plate. Do not bridge the gap with any solder as
this will result in a short circuit!
- Run the wires either though the hole where a neck string was or through the original buttonhole. Test the
stopwatch by touching the other ends of the wire together. The stopwatch should start or stop with each contact.
If so, place electrical tape over the connections so that nothing else will bridge the circuit. Reassemble the
stopwatch. If you soldered leads instead of the actual wires to the plates, solder the wires to the leads and
wrap electrical tape around them. For storing the device, wrap the wire around the spool or dowel.
- To make a switch, either take the pill container or the experimenter box and using the 3/8" drill bit,
drill a hole in the top. If 3/8" is too big or too small for your switch, use a different size. If you are
using a pill container, remove the plastic seal inside the cap before drilling. Insert the push-button switch
into the hole and secure it (fasteners are included). On the bottom or side of your container, use the
¼" drill bit to drill a hole for the wires to come out. If this drill bit is not the correct size for
your wires, use the appropriate one. Run the wires through the hole and solder them to the connections on the
switch. It is not necessary to tape these connections, as they will be enclosed in the box or pill container.
(See the schematic for more information.)
- Find a tall structure from which to drop pennies (30 40 at least). Attach the weight to the
string and drop the plumb bob. When the bob has reached the bottom and your partner notifies you of its doing
so, tighten the string and lower the measuring tape. If the tape does not reach the entire distance, find a
spot to stop the tape. Have your partner mark the spot and then measure from that spot. Repeat if necessary.
Once the tape has reached the bottom, have your partner hold the tape and tighten the tape. Record your
measurement. The accuracy can be a little slack because a difference of 1" or so will hardly be detected
by the times. Wind up all measuring devices.
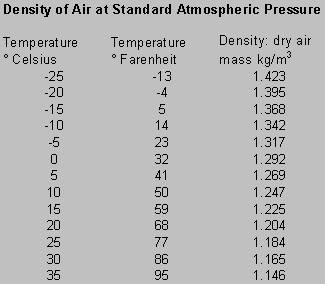
- Measure the temperature. This will be helpful in determining the air density.
- Drop the stopwatch end (that is, keep the switch) to the bottom. When both partners are ready, begin
dropping pennies. Push the switch to start the stopwatch the instant you release the penny. When the other
partner sees the penny hit the ground. Record time of fall. Repeat with different types of pennies
and different ways of dropping them (e.g. rolling or flat). Be sure to note which way the penny was dropped
and which type of penny it was.
- After several trials involving pennies, switch to the ball bearings. Then, repeat dropping pennies and
ball bearings at different heights.
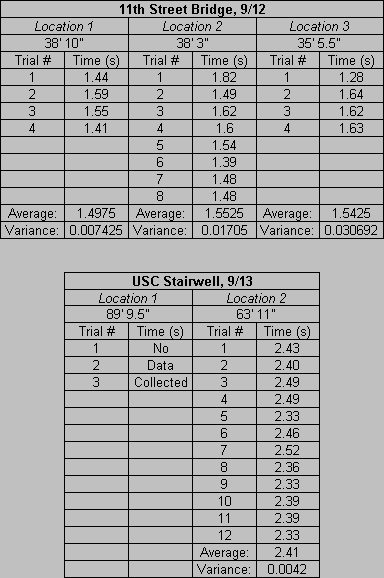
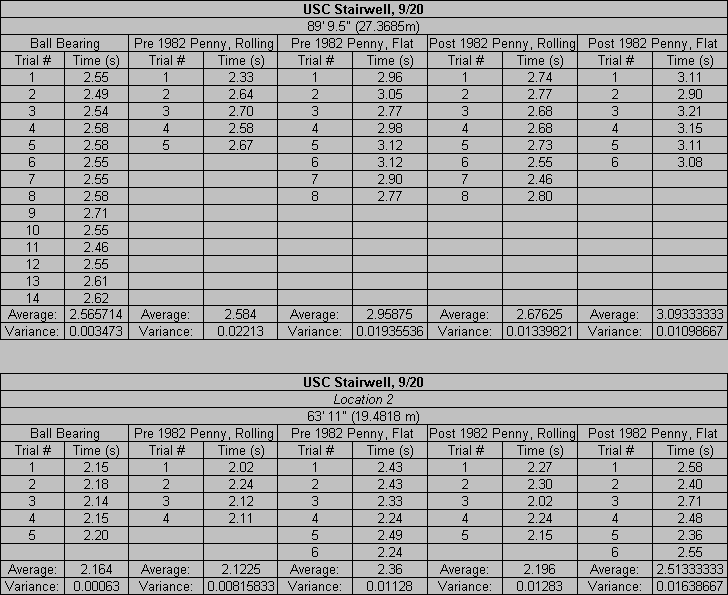
DATA: Eleventh Street Bridge data collected at approximately 77° F while USC data collected at
approximately 86° F. Altitude of both trials is approximately 4600 feet above sea level.
CALCULATIONS:
The drag force on an object is given by the equation
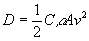
where D is the drag force, C is the drag coefficient usually in the range of 0.5 1.0, rho
is the density of air, A is the effective cross-sectional area of the falling body, and v is
the speed of the fall. At terminal velocity, the drag force will be equal to the weight of the object, that is,
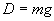
Thus,
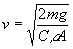
To calculate the air density, use the following table [2],
As suggested in the article "Chaotic dynamics of falling disks" [3], the
penny will fall in one of four ways depending on how it is dropped. These different paths are steady (falling
flat straight down), periodic (oscillating from side to side), chaotic, and tumbling. The flat penny should
have fallen either flat or periodic and the rolling penny either chaotic or tumbling. Due to the extreme
differences in the path of these falls and the inability to categorize appropriately the fall, actual
calculations become very difficult. Consequently, the drag coefficient cannot be accurately determined. Even
if it could, it would be a function of time relating to the fall of the penny. The average value of this
function would probably be useful for an approximation of the terminal velocity. Hopefully, the falling times
and positions (rolling or flat) collected in this experiment will be of assistance to someone in determining an
effective cross-sectional area or a drag coefficient. If either of these properties is found, please e-mail
macklem@colorado.edu. Until then, comparison with a table [4] of known terminal velocities should be adequate.
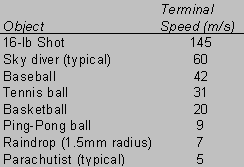
CONCLUSION: Reject the hypothesis and instead accept that a penny falling at terminal velocity will
not kill a person. After reviewing the table of terminal velocities, a penny may fall faster than a Ping-Pong
ball, but certainly not any faster than a basketball. These terminal velocities convert to about 20-45 mph
(32-72 kph). This may cause a bit of a sting, but it is not going to kill a person. For further confirmation,
Dennis Thompson tells about dropping pennies in a vacuum [5]. He says the pennies simply bounce several feet
high, but the impact leaves no visible marks on the penny. Although the fall from the Empire State Building
is three times that of the vacuum chamber, a penny certainly will not fall faster in air than in this chamber
thus making pennies non-lethal.
DISCUSSION OF ERROR: For the measurements taken in the USC Stairwell on September 13, air conditioners
were running in the building. Consequently, air drafts in the stairwell may have skewed the data to represent
longer or shorter than actual falling times.
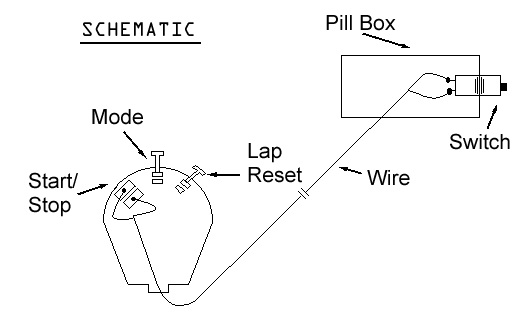
DIAGRAM: Because you will modify the way in which the stopwatch is operates, it is important to note
how to use the stopwatch. This will cover the operation of a modified stopwatch similar to the one pictured on
the first page of the procedure. The two separate wires soldered to the internal components of the stopwatch
replace the need of the button. When these two wires are connected, the stopwatch behaves as if the button
were pushed. The reason another button is connected to the wires is to ease the operation of the stopwatch.
The main unit will be at the bottom of the drop site for the second partner to stop the stopwatch. The first
person will have the new button and the wire will be between the partners. When the first partner drops the
penny, he will also click the button starting the timer. When the second partner sees (not hears) the
penny hit the ground, he should hit the pause button (also called lap reset). This is the time it takes for
the penny to fall. Of course, the stopwatch is still counting. After assuring the second partner has recorded
the time of the fall, the first partner must then click his button again to stop the watch. Then the second
partner will need to press the lap reset button once more to revert back to the timing of the stopwatch and
finally the clear button.
REFERENCES:
- http://www.ustreas.gov/opc/opc0075.html
- http://www.windpower.dk/stat/unitsw.htm#anchor138877
- Field, Stuart B., Klaus, M. & Moore, M.G. Chaotic dynamics of falling disks. Nature.
388, 252-254 (1997).
- Halliday, David & Resnick, Robert. Fundamentals of physics. Third Ed. (1988).
Original Source: Adapted from Peter J. Brancazio, Sport Science,
Simon & Schuster, New York, 1984.
- http://www.urbanlegends.com/science/penny_falling_impact.html





![]()
![]()
![]()


